
Marcelo Finger Alan Barzilay



LSTM & GRU
Parte 1
Roteiro
- Conceitos de Álgebra Linear
- LSTMs
- GRUs
- Redes Bidirecionais

Revisão Rápida de Conceitos de Álgebra Linear

Produto Escalar

\(\vec{u} \cdot \vec{v} = \displaystyle \sum_{i=1}^n u_i v_i = \left | \vec{u} \right | \left |\vec{v}\right| cos(\theta) \)
Notações alternativas: \(\langle \vec{u},\vec{v}\rangle\),\(\vec{u} \cdot^{T} \vec{v}, \vec{u}^T \cdot \vec{v}, \vec{u}' \cdot \vec{v}\)
Projeção de \(u\) sobre \(v\)
Operação básica da multiplicação de matrizes: \(C = A \times B\)
\(c_{ij} = \mathit{linha}_i(A) \cdot \mathit{coluna}_j(B) = A_i \cdot B^j\)
Produto Vetorial
\vec{a} \times \vec{b} = \begin{vmatrix}
\vec{i}& \vec{j}&\vec{k} \\
a_x& a_y & a_z\\
b_x& b_y &b_z
\end{vmatrix}
O resultado é um vetor ortogonal a \(\vec{a}\) e \(\vec{b}\): regra do polegar direito, espaço tri-domensional
Pouco utilizado em redes neurais

Produto de Hadamard
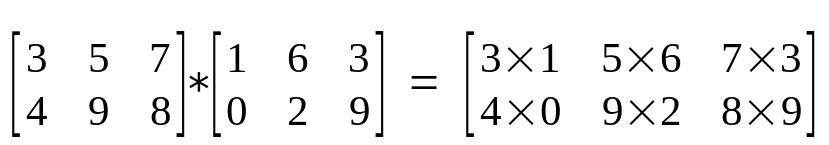
Produto item a item

