Marcelo Finger Alan Barzilay



RNN's
Parte 03: Modelos Sequência para Sequência
Conteúdos
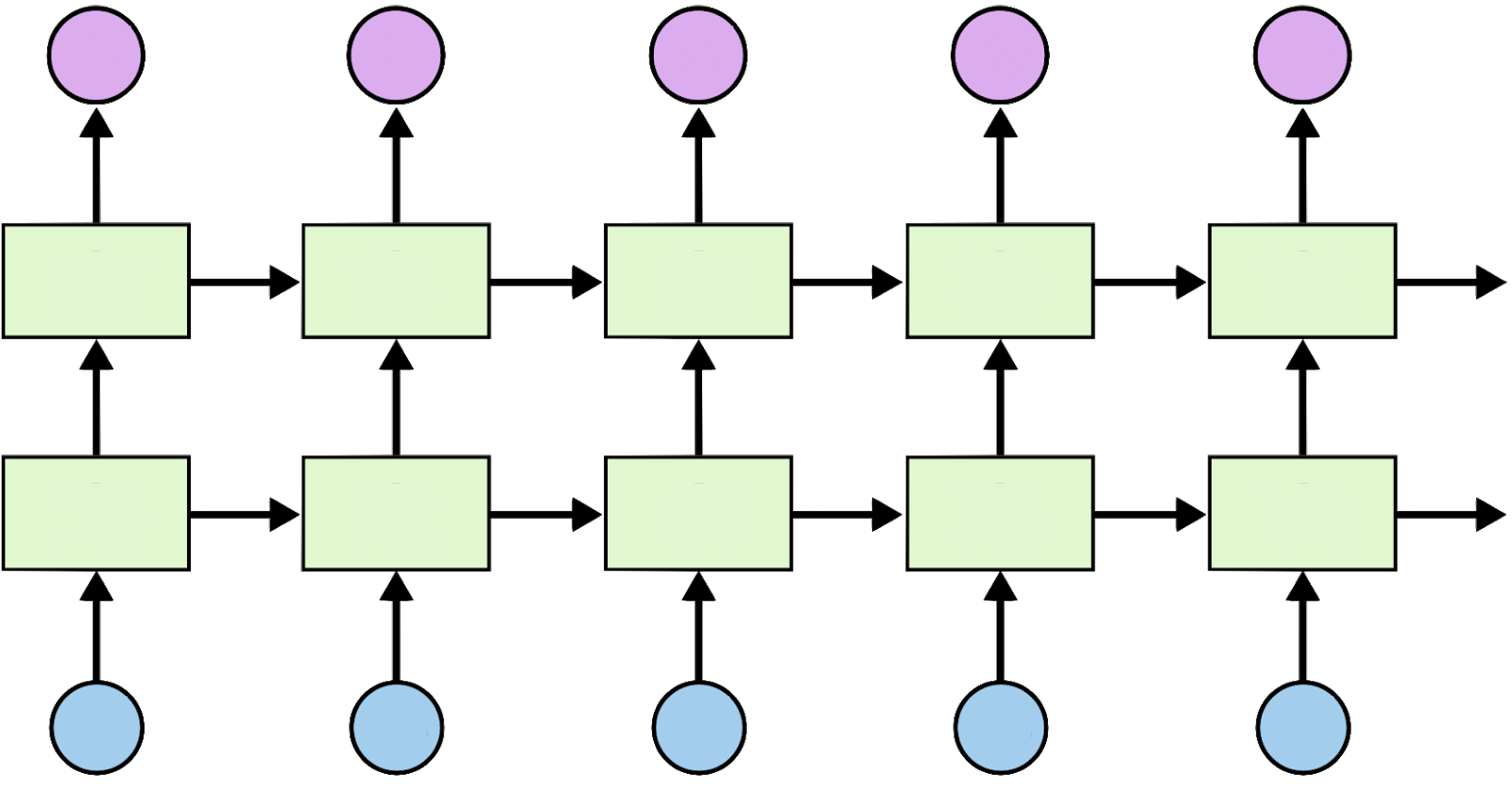
- Recorrência Neural
- Treinamento Recorrente
- Modelos Sequência pra Sequência
- Problemas que Advem da Recorrência
- Soluções para Redes Profundas

Modelo Sequence-to-Sequence

Seq2Seq
Diversas tarefas de PLN lidam com sequências:
-
Tradução (Machine Translation)
-
Responder perguntas (Q&A)
-
Reconhecimento de fala (Speech Recognition): tradução de áudio para texto

Seq2Seq
RNN’s são capazes não somente de processar sequências como também de gerar sequências.
Uma arquitetura popular para tarefas Seq2Seq é a arquitetura Encoder Decoder.

Encoder Decoder
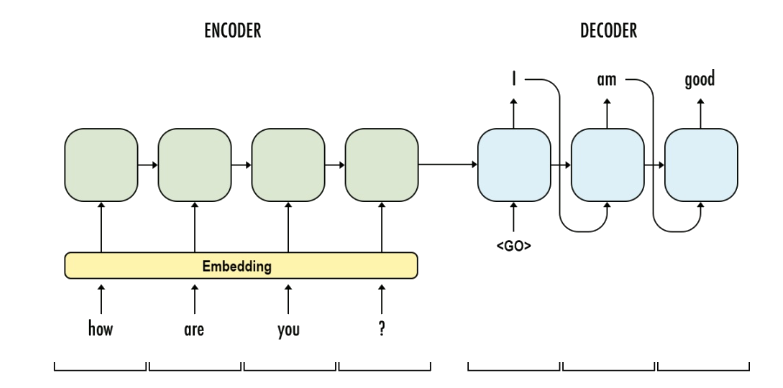
Redes Encoder Decoder possuem 2 partes:
-
Uma RNN chamada encoder que recebe uma sequência de tamanho qualquer e gera uma codificação: um vetor C de tamanho fixo.
-
Uma RNN chamada decoder que recebe o vetor C e gera uma sequência de tamanho qualquer, auto-regressivamente

Encoder Decoder
Redes Encoder Decoder possuem 2 partes:
-
Uma RNN chamada encoder que recebe uma sequência de tamanho qualquer e gera uma codificação: um vetor C de tamanho fixo.
-
Uma RNN chamada decoder que recebe o vetor C e gera uma sequência de tamanho qualquer.
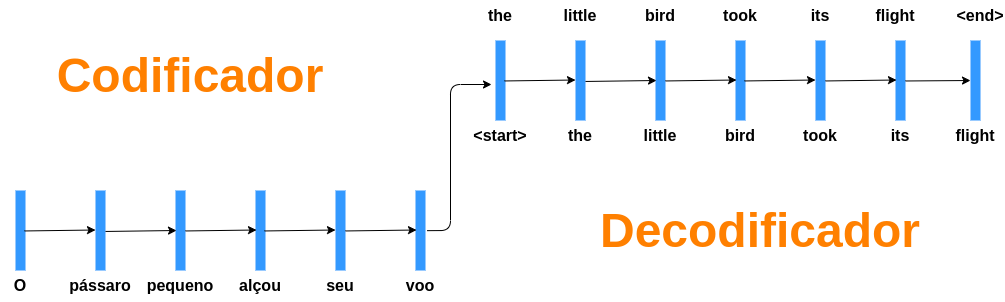

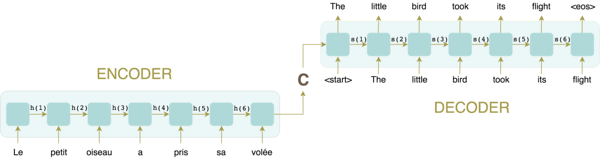
Encoder Decoder
O decoder recebe o último token gerado até prever um token especial <eos> que representa o fim de uma frase.

Possibilita a geração de um modelo neural de linguagem
Auto-Alimentação do Decoder

Encoder: uma rede recorrente

Decoder: rede recorrente + c

Multiplicidade de Inputs e Outputs
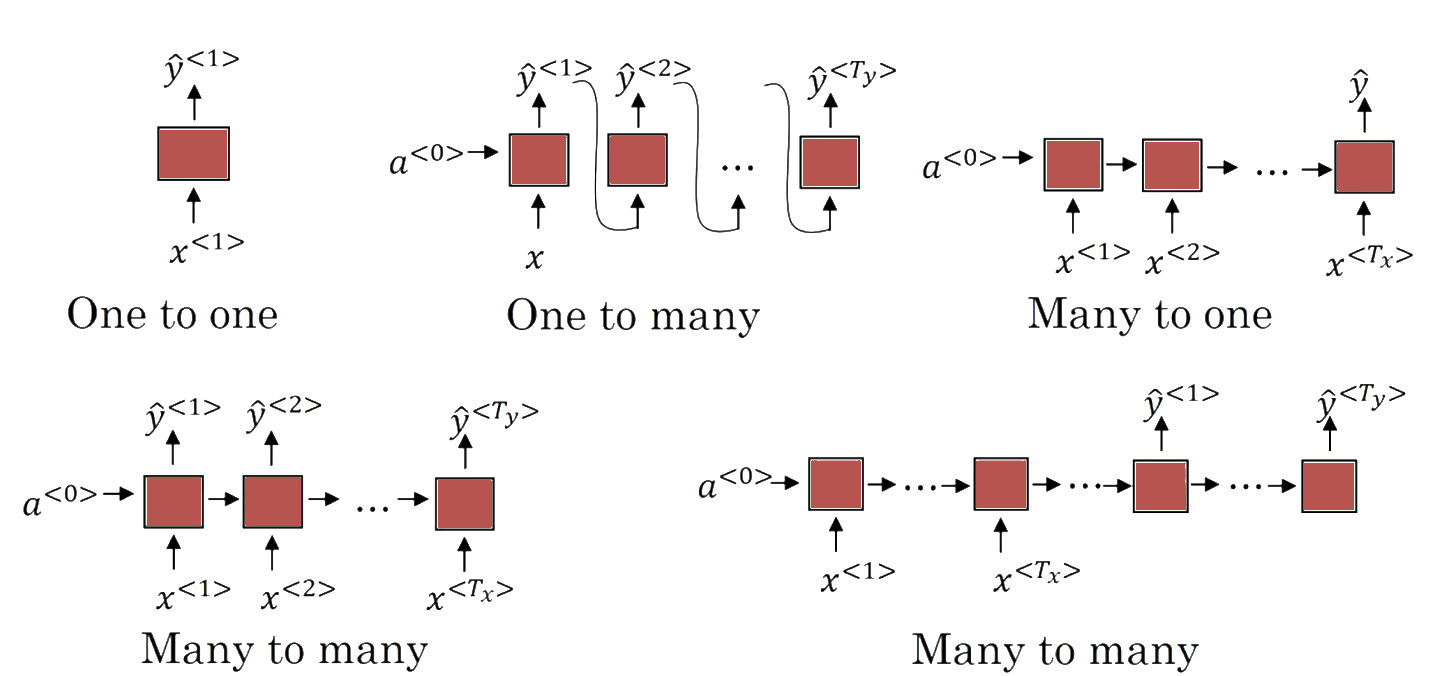
\(T_x \neq T_y\) (Encoder-Decoder)
\(T_x=T_y\)


Ainda podemos adicionar camadas extras