Word2vec
Parte 03: Modelo CBOW Completo

Marcelo Finger Alan Barzilay



Tópicos
- O Modelo Básico
- Detalhamento Formal
- Modelo CBOW Completo
- Otimizações no Modelo CBOW
- Formas de Avaliar o Word2vec
- Outro Embeddings Pré-treinados


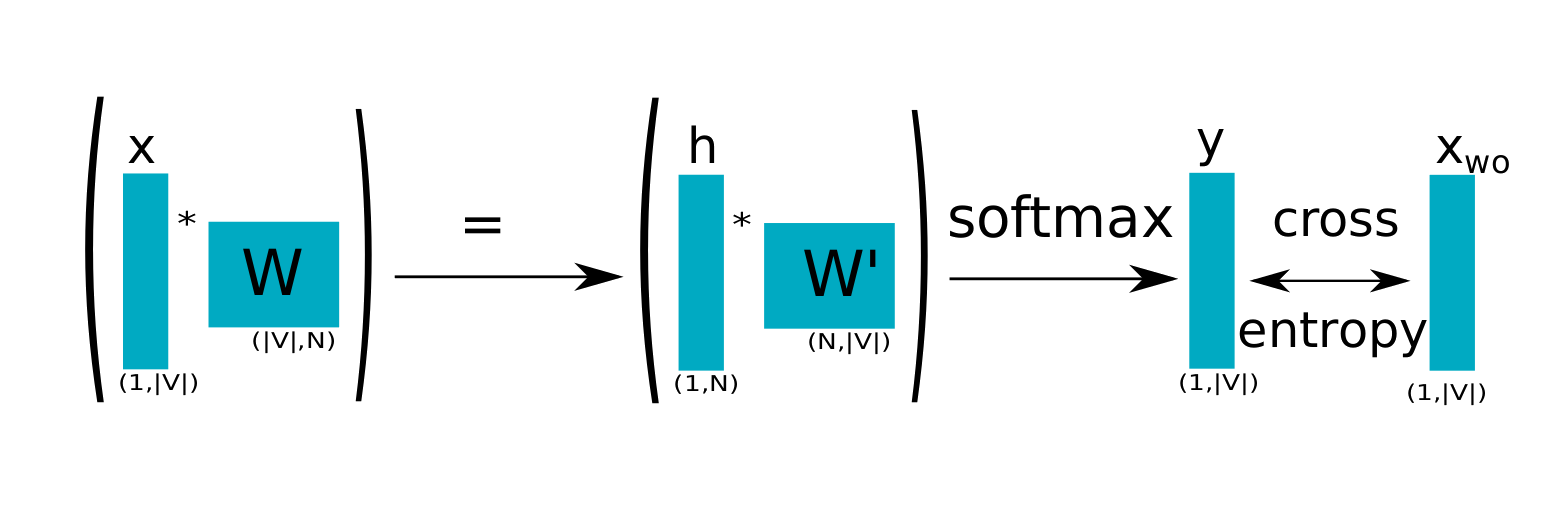
CBOW será completado
A partir de uma janela arbitrária de tamanho \(C\), construímos observações como \(([p_ {e}^1, \dots, p_ {e}^C], p_ {s})\).
Por exemplo, para \(C = 4\):
Nunca me acostumei com o cantor dessa banda, e nem ...
([com, o, dessa, banda], cantor)


CBOW Completo Esquematizado
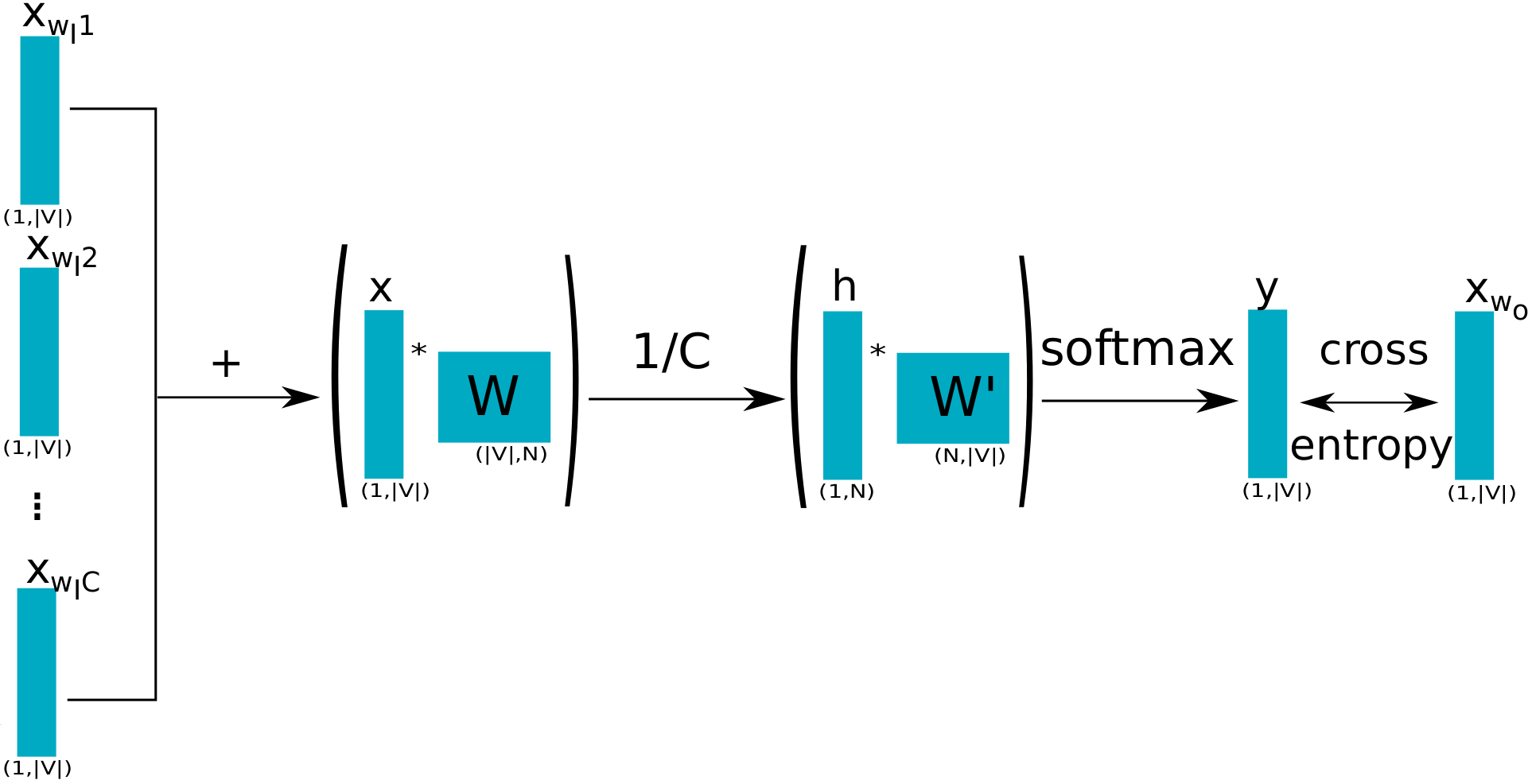
\[ x= x_{p_{e}^1} + \dots + x_{p_{e}^C}\]
\[h = \frac{1}{C}(W \cdot x) \]
\[u = W' \cdot h\]
\[y_j = P(p_{j}|p_e^{1},\dots, p_e^{C}) = \frac{\exp(u_{j} )}{\sum_{k=1}^{m}\exp(u_{k})} \]
\[\lambda= CE(u,y) = - u_{s} + \log \left(\sum_{k=1}^{m} \exp (u_{k})\right)\]

CBOW Completo: o modelo
O cálculo de \(\lambda\) é computacionalmente caro pois \(m\) é muito grande
\[{W^{\prime}}^{(new)} = {W^{\prime}}^{(old)} - \alpha \, \lambda \, h^T\]
\[{W}^{(new)} = {W}^{(old)} - \frac{\alpha}{C} \, DW'\]
onde \(D\) é a matriz diagonal com \(d_{ii} = y_i, i \neq s\) e \(d_{ss}=y_s -1\).

CBOW Completo: atualização
O cálculo da função softmax é muito caro para cada entrada do treinamento:
\[y_j = \frac{\exp(u_j)}{\sum_{k=1}^{m} \exp(u_{k})} \]
Técnicas de PLN (probabilísticas) se fazem necessárias. Duas alternativas que aproximam \(y\), e otimizam o tempo
- Amostragem Negativa
- Softmax Hierárquica

