Word2vec
Parte 01: O Modelo Básico

Marcelo Finger Alan Barzilay



Tópicos
- O Modelo Básico
- Detalhamento Formal
- Modelo CBOW Completo
- Otimizações no Modelo CBOW
- Formas de Avaliar o Word2vec
- Outro Embeddings Pré-treinados

Word2vec
- Objetivo: pré-treinar uma representação vetorial das palavras
\[banana \longrightarrow \left\langle v_1, \ldots, v_N\right\rangle, v_i \in \mathbb{Q}\]
- Aprendizagem não-supervisionada, a partir de um grande córpus
- Baseado em co-ocorrências estatísticas. Uma ideia antiga:
Uma palavra é conhecida pela companhia que mantém (J.R. Firth, 1957)
- Na verdade, são 2 modelos:
- Skip-gram
- Continuous Bag-of-Words (CBOW)

Iniciar por CBOW Simplificado
A tarefa é predizer o vetor da palavra-foco dado um contexto de palavras:
O primeiro rei de Portugal nasceu em ...
Observação: (rei, primeiro)
(entrada, saída)
(contexto, foco)
(\(w_e\), \(w_s\))

Formalizando CBOW Simplificado
Dado um córpus, escolher:
- Um vocabulário \(V\), de tamanho \(m\)
- Um tamanho \(n\) para representar as palavras
Duas matrizes \(W\) (\(m \times n\)) e \(W'\) (\(n \times m\)) para criar duas representações associadas a uma palavra \(p\):
- um vetor de entrada: \(w_p\) (linha de \(W\))
- um vetor de saída: \(w'_p\) (coluna de \(W'\)
A representação final da palavra \(p\) será \(w_p\)


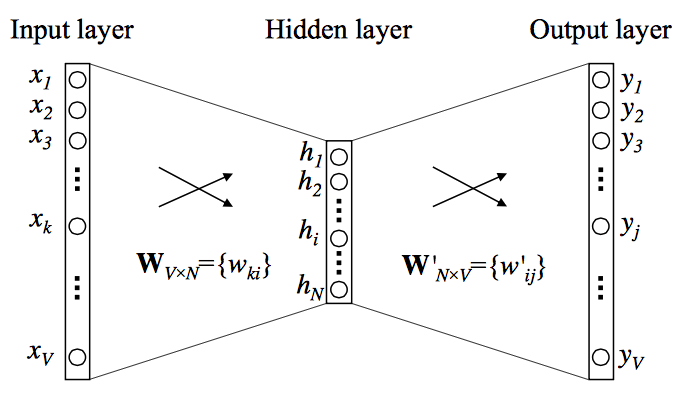
Deep Learning sem ativação com profundidade 2 (na verdade 1,5) !
CBOW Esquematizado

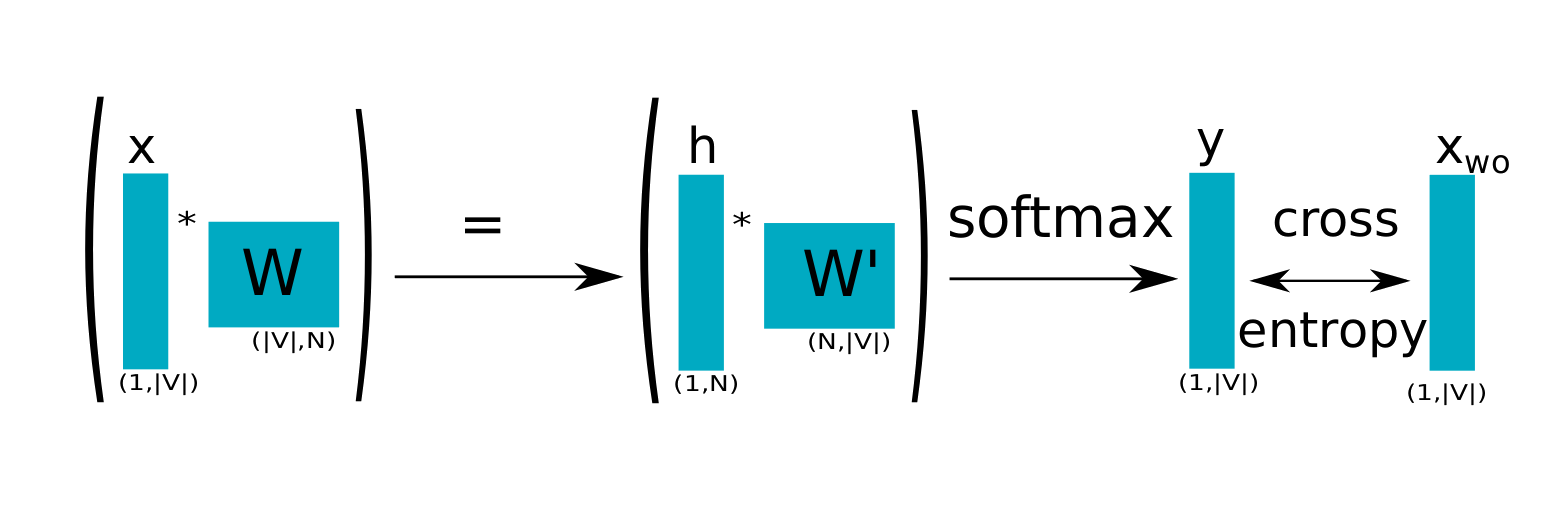
Definições
Representação one-hot é um vetor de bits com apenas um bit-1; todos os outros bits são 0:
\[\langle 0, \cdots, 0 , 1 , 0 , \cdots, 0 \rangle\]
A função softmax é uma distribuição de probabilidade sobre os elementos de um vetor \(z\):
\[P(z_j) = \frac{e^{z_j}}{ \sum_{i=1}^N e^{z_i}} \in [0,1], \qquad z_j \in \mathbb{Q}\]
A entropia-cruzada de distribuições \(p\) (original) e \(q\) (estimada):
\[ CE(p,q) = -\sum_i p_i \log q_i \]

