Introdução às Redes Neurais

Marcelo Finger
Alan Barzilay

Parte 04 - Treinamento

Função custo (Loss)

Utilizando um modelo chegamos em uma previsão ŷ, como saber se esta é uma boa previsão?

No aprendizado supervisionado, há dados de treinamento \((x_1,y_i), \ldots, (x_n, y_n)\)

Função custo (Loss)

A função custo é responsável por quantificar o quão distante nossa previsão esta do valor esperado, quanto maior o custo, pior a previsão.

Logo, a otimização de nosso modelo pode ser formulada como uma minimização da função custo.

\(Loss = f(\hat{y},y)\)

Função custo (Loss)

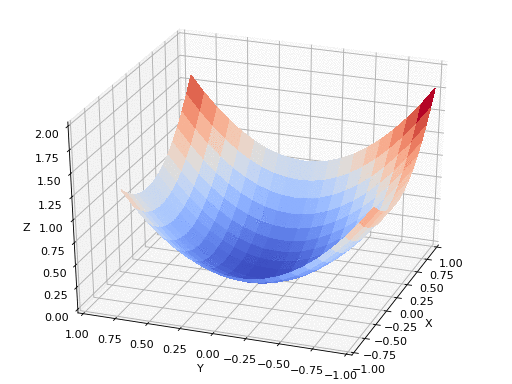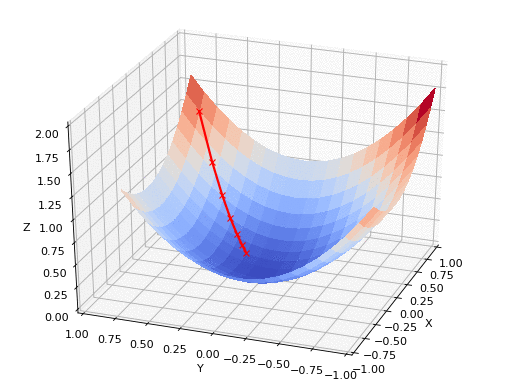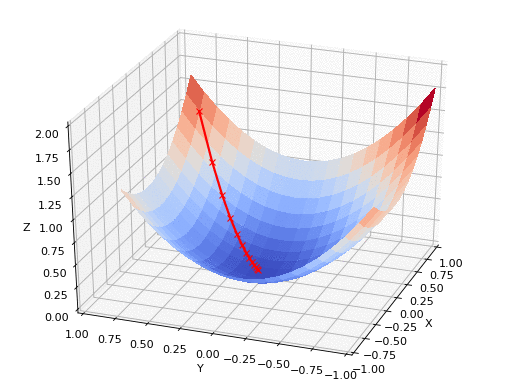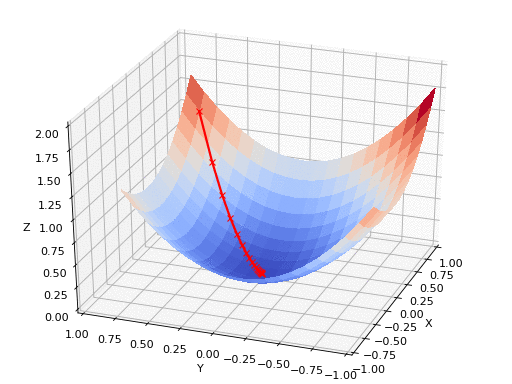
Uma estratégia comum é caminhar no sentido contrario ao do gradiente para encontrar um mínimo da função custo:

Essa estratégia é conhecida como gradiente descendente

\(\alpha\): taxa de aprendizado

w^{s+1} = w^s - \alpha \cdot \nabla J

Função custo (Loss)

A funcão custo nem sempre é convexa, podemos encontrar um mínimo local ao invés de um mínimo global

Como treinar uma rede neural pelo gradiente descendente?

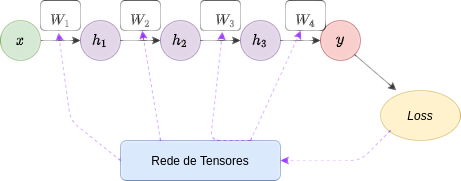
Backpropagation

O algoritmo de backpropagation pode ser dividido em 3 partes:

passo para frente, com os pesos atuais
calculo da loss
passo para trás, atualizando os pesos

Backpropagation

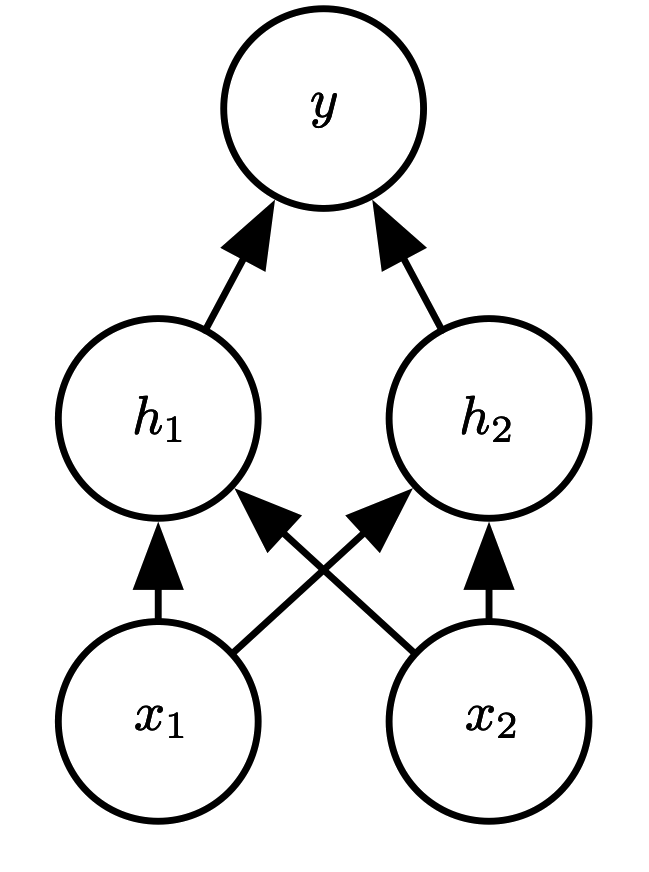
Cálculo da loss(\(\hat{y},y\))

passo para frente

passo para trás

Backpropagation

Quando propagamos para trás o gradiente do custo, nós nos utilizamos da regra da cadeia para percorrer a rede

\frac{\partial \mathfrak{L}}{\partial w} =\frac{\partial \mathfrak{L}}{\partial h_2}\frac{\partial h_2}{\partial h_1}\frac{\partial h_1}{\partial w} \\[1em] w_{ij}^{k^{s+1}} := w_{ij}^{k^s} - \alpha \frac{\partial \mathfrak{L}}{\partial w_{ij}^k}

Rede de Tensores

Uma rede de Tensores é automaticamente construída para ser usada na atualização dos pesos durante o treinamento

Para se aprofundar

Imagem de um botão estilizado de volta para pagina inicial