Introdução às Redes Neurais

Marcelo Finger Alan Barzilay



Parte 03 - Redes Multicamadas

XOR
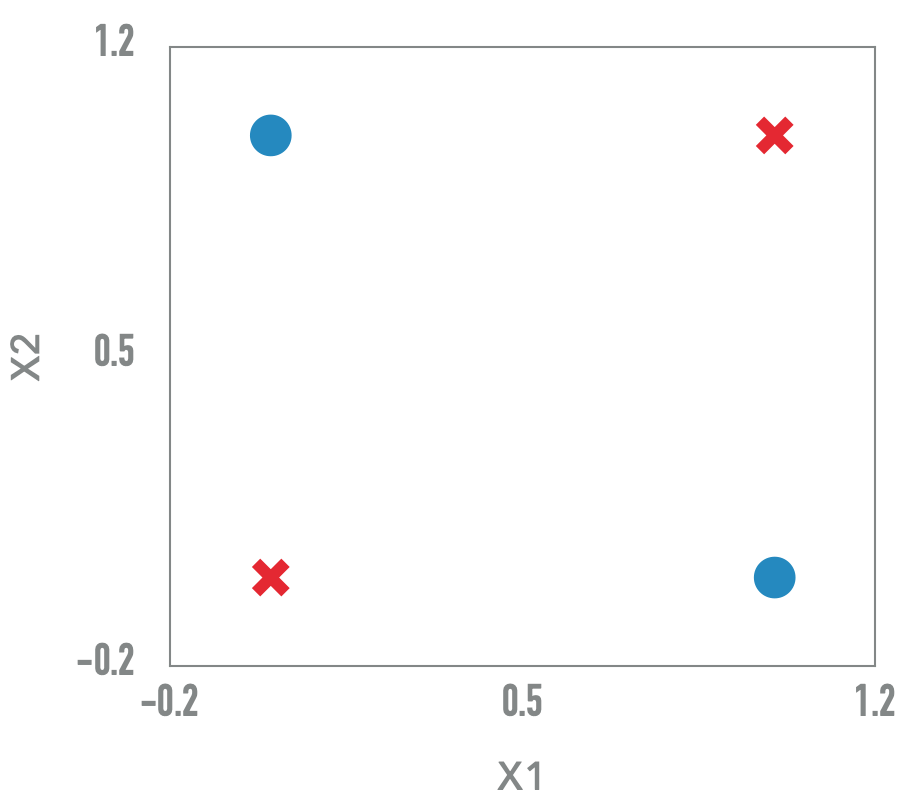
Perceptron Clássico e incapaz de aprender a função booleana XOR
Mas e com 2 hiper-planos?
Uma combinação linear de modelos lineares resultará em um modelo linear.
Como introduzir não linearidade?

Um Neurônio Artificial
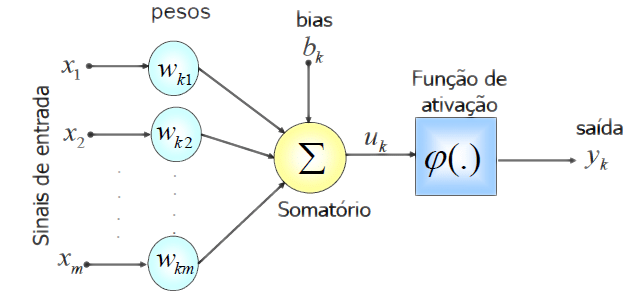
- Entrada: \(x = [x_1, \ldots, x_m]\)
- Parâmetros: \([w_{k1}, \ldots, w_{km}]\), viés \(b_k\)
- \(u_k =b_k + \sum_{i=1}^{m} w_{ki}x_i\)
- Saída: \(y_k = \varphi(u_k)\)
Adaptado de P. Soares e J. P. Silva, RBCA 2011

Funções de ativação
- Sigmoide

Sigmoide

\sigma(x) = \frac{1}{1+e^{-x}}

Funções de ativação
- Sigmoide
- Tanh

Tanh

tanh(x) = \frac{e^x - e^{-x}}{e^x +e^{-x}}

Funções de ativação
- Sigmoide
- Tanh
- ReLU

ReLU

max(0,x)

Funções de ativação
- Sigmoide
- Tanh
- ReLU
- Leaky ReLU

Leaky ReLU

\begin{cases}
0.01x & se\ x \leq 0\\
x & se\ x > 0
\end{cases}


Perceptron Multicamada
Hornik 1989: Perceptrons multicamada com funções de ativação (não lineares) podem aproximar arbitrariamente bem qualquer função continua
Combinando diferentes perceptrons podemos construir uma rede que resulta em um modelo fundamentalmente mais poderoso
Rede Neural Feed-Forward Multicamada
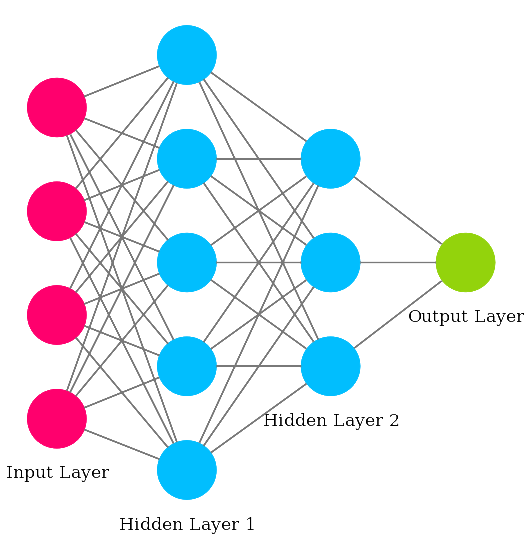
- Cada nó é um neurônio artificial
- Camadas intermediárias são chamadas de ocultas (hidden)

Visão Matricial das Redes Neurais
- Cada camada pode ser vista como uma matriz
- \(h_i = \varphi(W_i h_{i-1})\)
- \(h_0 = x\)
- \(y = h_{\mathit{ultima}}\)

- As matrizes de pesos \(W_i\) devem ser aprendidas

