Introdução às Redes Neurais

Marcelo Finger Alan Barzilay



Parte 02 - Perceptrons Probabilísticos

Problemas com Perceptron Clássico
- Separabilidade: se dados não são linearmente separáveis o algoritmo não converge
- Margens pequenas: O hiperplano gerado pode ter uma margem baixa o que leva a uma baixa generalização
- Nenhuma medida de confiança

Perceptron Probabilístico
(Regressão Logística)
Intuição: Quanto mais longe do hiper plano, maior a confiança na classificação
Esta intuição nos permite tratar de casos não separáveis
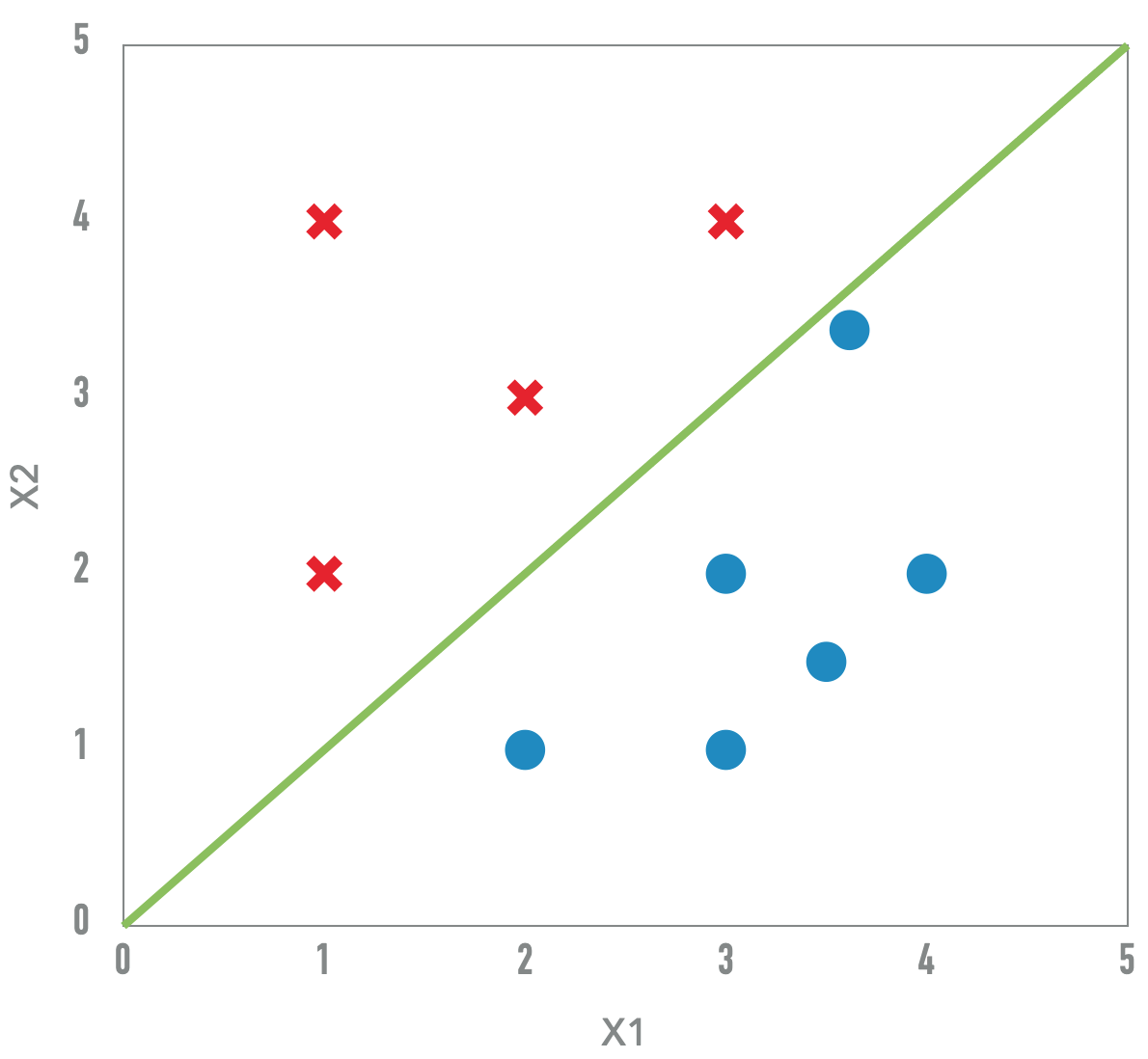

Perceptron Probabilístico
\Pr( Y=1|x) =0.5
\Pr( Y=1|x) \approx 0
\Pr( Y=1|x) \approx 1

x \cdotp w

Perceptron Probabilístico
\Pr( Y=1|x) =0.5
\Pr( Y=1|x) \approx 0
\Pr( Y=1|x) \approx 1

x \cdotp w
\Pr( Y=y|x) =\frac{1}{1+\ \exp( -y\cdotp w\cdotp x)}
\Pr( Y=1|x)

Problemas com Perceptron Clássico
- Separabilidade: se dados não são linearmente separáveis o algoritmo não converge
- Margens pequenas: O hiperplano gerado pode ter uma margem baixa o que leva a uma baixa generalização
- Nenhuma medida de confiança

Não-linearidade e Separabilidade
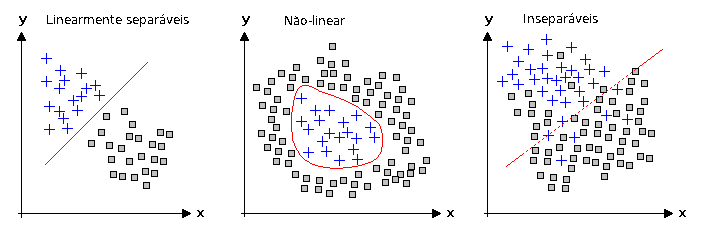
Sempre existe uma transformação não-linear que separa os dados
Mas, essa transformação pode ser computacionalmente cara

Dados não linearmente separaveis
- Introduzir não-linearidade pode tornar nossos modelos mais "poderosos"
- Uma camada de separação nem sempre é suficiente
E se juntarmos essas 2 ideias?
Percéptrons multicamada com funções de ativação não lineares