Modelos Probabilísticos

Marcelo Finger
Alan Barzilay

O que é probabilidade?

  • Um resumo de toda uma configuração
  • Modelos probabilísticos possuem um conjunto de probabilidades como parâmetros:

{  P( A|B,C,D ) = p }

Cadeias de Markov

Cadeias de Markov

  • Modelo Probabilístico que enxerga fenômenos como uma transição entre estados
  • Hipótese de Markov:
P(X_{i+1}|X_i, X_{i-1},\ldots,X_{i-k}) = P(X_{i+1}|X_i)

"A probabilidade de transição para o próximo

estado depende apenas do estado atual"

Cadeia de Markov em Geral

Cadeia de Markov em PLN

ori \ dest D N V P
D 0,01 0,80 0,18 0,01
N 0,05 0,30 0,40 0,25
V 0,30 0,25 0,20 0,25
P 0,30 0,30 0,30 0,1

Etiquetagem Morfossintática

Cadeia de Markov de Ordem 2

ori \ dest D N V P
DD 0,001 0,800 0,188 0,001
DN 0,005 0,300 0,400 0,255
DV 0,300 0,250 0,200 0,250
DP 0,303 0,302 0,304 0,091
ND ... ... ... ... ...

Etiquetagem Morfossintática

Cadeia de Markov em PLN

  • Encontrar a sequência mais provável e escolhê-la (Algoritmo de Viterbi)
  • Facilmente expansível para sequências de 2, 3, 4
  • Tamanho da Janela
  • Complexidade exponencial no tamanho da janela
  • Insensível ao mundo fora da janela

Modelos de n-gramas

Ideia Básica

  • Ignorar a sequência de palavras no texto
  • Considerar o texto como um multi-conjunto:

elemento, contagem

  • Cada elemento é uma sequência de n tokens
  • Saco de palavras (bag of words)                   

Texto

Atirei o pau no gato

Mas o gato não morreu

Unigrama (n=1)

atirei: 1

gato: 2

mas: 1

morreu: 1

não: 1

no: 1

o: 2

pau: 1

Texto

Atirei o pau no gato

Mas o gato não morreu

atirei o: 1

o pau: 1

pau no: 1

no gato: 1

gato mas: 1

mas o: 1

o gato: 1

gato não: 1

não morreu: 1

Bigrama (n=2)

Texto

Atirei o pau no gato

Mas o gato não morreu

Trigrama (n=3 )

<ini> atirei o: 1

atirei o pau: 1

o pau no: 1

pau no gato: 1

no gato mas: 1

gato mas o: 1

mas o gato: 

o gato não: 1

gato não morreu: 1

não morreu <fim>:1

Exemplo de Aplicação

  • Análise de sentimento
  • Cáculo da probabilidade do sentimento condicionado nos elementos do bigrama
\begin{array}{rcl} P(\textrm{sentimento}=\textit{positivo} | \texttt{atirei o})& = & 0.1\\ P(\textrm{sentimento}=\textit{neutro} | \texttt{atirei o})& = & 0.2\\ P(\textrm{sentimento}=\textit{negativo} | \texttt{atirei o})& = & 0.7 \end{array}
\textrm {Sentimento texto} = \argmax_{\textit{sentimento}} \displaystyle \prod_{\textit{bigrama} \in \textit{Texto}} P(\textit{sentimento}|\textit{bigrama})

Aprendizado supervisionado

  • Córpus de treinamento: coleção textos cujo sentimento já foi classificado: 
\begin{array}{l} P(\textit{sentimento}|\textit{bigrama}) = \\ \qquad \displaystyle \frac{\textrm{Conta}(\textit{bigrama} \in \textit{texto classificado por sentimento})} {\textrm{Conta}(\textit{bigrama} \in \textit{corpus})} \end{array}

Gramáticas Probabilistas

Gramática Ambígua

Gramática Probabilista

\begin{array}{ll} S &\longrightarrow SN~ SV\\[1ex] SN &\longrightarrow Det~ N\\ SN &\longrightarrow PRO \\ SN &\longrightarrow SN~ SP \\[1ex] SV &\longrightarrow VI\\ SV &\longrightarrow VTD~ SN\\ SV &\longrightarrow VTI~ SP\\ SV &\longrightarrow VTDI~ SN SP \end{array}
\begin{array}{lll} S &\longrightarrow SN~ SV & 1.0\\[1ex] SN &\longrightarrow Det~ N & 0.2\\ SN &\longrightarrow PRO & 0.1\\ SN &\longrightarrow SN~ SP & 0.7\\[1ex] SV &\longrightarrow VI & 0.3\\ SV &\longrightarrow VTD~ SN & 0.4\\ SV &\longrightarrow VTI~ SP & 0.2\\ SV &\longrightarrow VTDI~ SN SP & 0.1 \end{array}

Probabilidade de Árvores Sintáticas

eu      vi      o       menino      com      o        telescópio

D               N

D            N              P                 SN

SN                            SP

PRO   VT                             SN

SN                    SV

S

SN                            SP

P(Árvore1) = 0.01234

Escolhe a Estrutura de Maior Probabilidade

eu      vi      o       menino      com      o        telescópio

D            N                         D               N

PRO  

SN                                  SV

S

SV                                    SP

VT            SN                    P                SN

P(Árvore2) = 0.02468

Propriedades

  • Meta: resolver ambiguidades sintáticas
  • Prioriza estruturas de maior probabilidade.
  • Supõe independência entre regras
  • Incapaz de capturar as interdependências entre as expressões e seu contexto 

Modelos Probabilísticos Avançados

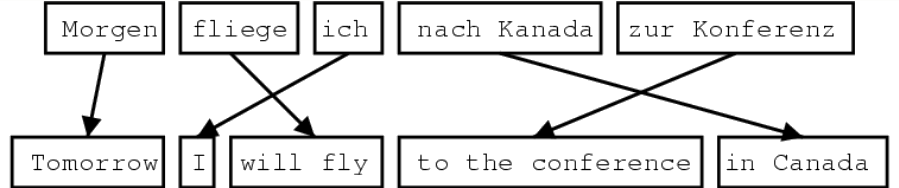
Alinhamento de Textos Paralelos

Modelo ultrapassado por tradução usando redes neurais com uma arquitetura encoder-decoder

Imagem de um botão estilizado de volta para pagina inicial